

专为程序员规划的线性代数课程
创新规划+通俗易懂,这一次,bobo教师带你完全学会线性代数!
bobo老师专为程序员规划的线性代数课程,全新的课程规划模式,配合编程讲解,回绝单调的例题讲解,而是讲清楚每一个常识点的来龙去脉,完好学习线性代数领域的常识系统,这一次,让你学会线性代数!
合适人群
线性代数怎么学都不会的同学;大学学过线性代数,
可是考完试就忘记,不能真实运用线数的同学;
想深入学习人工智能,机器学习,深度学习等领域,
却苦于自己数学根底欠好的同学。
技术储备要求
高中数学根底;
编程部分需求Python3语言根底。
(其他语言,如Java,C++等也可以运用)
[wm_notice]试看链接:https://pan.baidu.com/s/1mV2Bj-kwnOeUFTVSELW4sg
提取码:gex2
–来自百度网盘超级会员V1的分享容[/wm_notice]
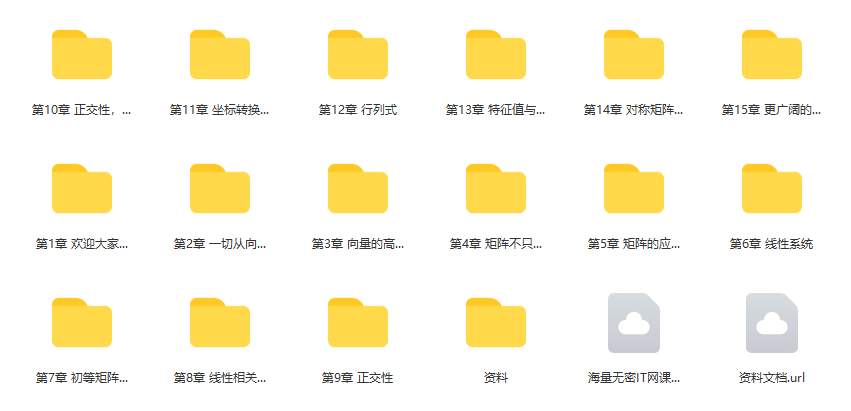
章节目录:
-
第1章 欢迎咱们来到《专给程序员规划的线性代数》4 节 | 61分钟
欢迎咱们来到《专给程序员规划的线性代数》,在这个课程中,咱们将运用编程的方式,学习线性代数,这个近现代数学发展中最为重要的分支。学懂线性代数,是同学们深化学习人工智能,机器学习,深度学习,图形学,图画学,密码学,等等许多范畴的根底。从这个课程开端,让咱们真正学懂线性代数!…
- 视频:1-1 《专为程序员规划的线性代数课程》导学 (14:51)
- 视频:1-2 课程学习的更多补充说明 (17:55)
- 视频:1-3 线性代数与机器学习 (13:21)
- 视频:1-4 课程运用环境树立 (14:14)
-
第2章 全部从向量开端 试看9 节 | 98分钟
向量,是线性代数研讨的根本元素。在这一章,咱们将引进向量。什么是向量?咱们为什么要引进向量?从而,咱们将运用不同的视角看待向量,界说向量的根本运算,领会数学研讨进程中,从底层开端,一点一点向上树立数学大厦的进程:)…
- 视频:2-1 什么是向量. (16:11)试看
- 视频:2-2 向量的更多术语和表明法 (08:15)试看
- 视频:2-3 完成属于咱们自己的向量 (12:41)试看
- 视频:2-4 向量的两个根本运算. (09:38)
- 视频:2-5 完成向量的根本运算. (16:05)
- 视频:2-6 向量根本运算的性质与数学大厦的树立. (10:47)
- 视频:2-7 零向量. (16:24)
- 视频:2-8 完成零向量 (03:30)
- 视频:2-9 全部从向量开端 (04:21)
-
第3章 向量的高档论题7 节 | 96分钟
在这一章,咱们将要点介绍向量的两个高档运算:规范化和点乘。对于点乘运算,咱们将深化了解其背面的几许意义,并且结合许多运用,了解点乘这个看起来奇怪的运算,背面的意义,以及在许多范畴的运用:)
- 视频:3-1 规范化和单位向量. (12:47)
- 视频:3-2 完成向量规范化 (15:54)
- 视频:3-3 向量的点乘与几许意义. (14:00)
- 视频:3-4 向量点乘的直观了解 (09:00)
- 视频:3-5 完成向量的点乘操作 (05:04)
- 视频:3-6 向量点乘的运用. (17:36)
- 视频:3-7 Numpy 中向量的根本运用 (21:17)
-
第4章 矩阵不只是 m*n 个数字11 节 | 157分钟
向量是对数的拓宽,矩阵则是对向量的拓宽。虽说线性代数研讨的根本元素是向量,但其实咱们更常看见矩阵!在这一章,咱们将深化矩阵,不只学习什么是矩阵,矩阵的运算等根底内容,更将从用更深化的视角看待矩阵:矩阵也能够看做是对一个体系的描绘;以及,矩阵也能够被看做是向量的函数!…
- 视频:4-1 什么是矩阵 (09:53)
- 视频:4-2 完成属于咱们自己的矩阵类 (16:15)
- 视频:4-3 矩阵的根本运算和根本性质 (11:54)
- 视频:4-4 完成矩阵的根本运算 (13:53)
- 视频:4-5 把矩阵看作是对体系的描绘 (21:54)
- 视频:4-6 矩阵和向量的乘法与把矩阵看作向量的函数 (16:01)
- 视频:4-7 矩阵和矩阵的乘法 (20:12)
- 视频:4-8 完成矩阵的乘法 (11:30)
- 视频:4-9 矩阵乘法的性质和矩阵的幂 (09:55)
- 视频:4-10 矩阵的转置 (10:28)
- 视频:4-11 完成矩阵的转置和Numpy中的矩阵 (14:24)
-
第5章 矩阵的运用和更多矩阵相关的高档论题10 节 | 124分钟
在咱们学习了矩阵之后,就现已能够将线性代数的常识运用在许多范畴了!在这一章,咱们将把线性代数具体运用在图形学中!同时,咱们将持续学习和矩阵相关的许多概念,如单位矩阵和矩阵的逆。最重要的是:咱们将揭示看待矩阵的一个重要视角:把矩阵看作是空间! …
- 视频:5-1 更多改换矩阵 (14:24)
- 视频:5-2 矩阵旋转改换和矩阵在图形学中的运用 (14:45)
- 视频:5-3 完成矩阵改换在图形学中的运用 (17:16)
- 视频:5-4 从缩放改换到单位矩阵 (10:47)
- 作业:5-5 简略的图形学改换
- 视频:5-6 矩阵的逆 (12:26)
- 视频:5-7 完成单位矩阵和numpy中矩阵的逆 (09:07)
- 视频:5-8 矩阵的逆的性质 (13:55)
- 视频:5-9 看待矩阵的关键视角:用矩阵表明空间 (22:24)
- 视频:5-10 总结:看待矩阵的四个重要视角 (08:42)
-
第6章 线性体系10 节 | 167分钟
线性体系听起来很巨大上,可是它的本质就是线性方程组!这个看似简略的形式,其实也隐藏着不小的学问,同时在各个范畴都被很多运用。在这一章,咱们将看到当引进矩阵,向量这些概念以后,求解线性方程组是多么的容易。…
- 视频:6-1 线性体系与消元法 (13:55)
- 视频:6-2 高斯消元法 (22:02)
- 视频:6-3 高斯-约旦消元法 (13:54)
- 视频:6-4 完成高斯-约旦消元法 (25:09)
- 视频:6-5 行最简形式和线性方程组解的结构 (23:09)
- 视频:6-6 直观了解线性方程组解的结构 (22:41)
- 视频:6-7 更一般化的高斯-约旦消元法 (17:03)
- 视频:6-8 完成更一般化的高斯-约旦消元法 (18:34)
- 视频:6-9 齐次线性方程组 (09:40)
- 作业:6-10 关于线性体系
-
第7章 初等矩阵和矩阵的可逆性9 节 | 178分钟
在上一章,咱们详细的学习了线性体系的求解。在这一章,咱们就将看到线性体系的一个重要的运用——求解矩阵的逆。千万不要小瞧矩阵的逆,一个矩阵是否可逆,和许多线性代数范畴的高档概念相关。在这一章,咱们也将一窥一二。同时,咱们还会学习初等矩阵的概念,同时,进入咱们在这个课程中将向咱们介绍的第一个矩阵分化算法…
- 视频:7-1 线性体系与矩阵的逆 (22:32)
- 视频:7-2 完成求解矩阵的逆 (10:24)
- 视频:7-3 初等矩阵 (20:45)
- 视频:7-4 从初等矩阵到矩阵的逆 (15:22)
- 视频:7-5 为什么矩阵的逆这么重要 (25:58)
- 视频:7-6 矩阵的LU分化 (25:58)
- 视频:7-7 完成矩阵的LU分化 (13:37)
- 视频:7-8 非方阵的LU分化,矩阵的LDU分化和PLU分化 (16:50)
- 视频:7-9 矩阵的PLUP分化和再看矩阵的乘法 (26:17)
-
第8章 线性相关,线性无关与生成空间9 节 | 145分钟
空间,或许是线性代数国际里最重要的概念了。在这一章,咱们将带领咱们逐渐了解,听起来巨大上又笼统的空间,究竟是什么意思?咱们为什么要研讨空间?空间又和咱们之前讨论的向量,矩阵,线性体系,等等等等,有什么关系。 …
- 视频:8-1 线性组合 (14:19)
- 视频:8-2 线性相关和线性无关 (22:14)
- 视频:8-3 矩阵的逆和线性相关,线性无关 (16:03)
- 视频:8-4 直观了解线性相关和线性无关 (21:31)
- 视频:8-5 生成空间 (16:03)
- 视频:8-6 空间的基 (22:40)
- 视频:8-7 空间的基的更多性质 (17:40)
- 视频:8-8 本章小结:构成自己的常识图谱 (14:04)
- 作业:8-9 关于总结
-
第9章 向量空间,维度,和四大子空间12 节 | 230分钟
在之前的线性代数的学习中,咱们一直在运用比如2维空间,3维空间,n维空间这样的说法,但究竟什么是空间,什么是维度,咱们却没有给出严格的界说。在这一章,咱们就将谨慎的来讨论,究竟什么是空间,什么是维度,从而,引申出更多线性代数范畴的中心概念。 …
- 视频:9-1 空间,向量空间和欧几里得空间 (18:26)
- 视频:9-2 广义向量空间 (18:28)
- 视频:9-3 子空间 (23:06)
- 视频:9-4 直观了解欧几里得空间的子空间 (16:50)
- 视频:9-5 维度 (21:48)
- 视频:9-6 行空间和矩阵的行秩 (20:48)
- 视频:9-7 列空间 (14:19)
- 视频:9-8 矩阵的秩和矩阵的逆 (17:25)
- 视频:9-9 完成矩阵的秩 (18:57)
- 视频:9-10 零空间与看待零空间的三个视角 (21:50)
- 视频:9-11 零空间 与 秩-零化度定理 (20:52)
- 视频:9-12 左零空间,四大子空间和研讨子空间的原因 (17:01)
-
第10章 正交性,规范正交矩阵和投影8 节 | 107分钟
信任,上一章对空间的讨论,现已推翻了咱们对空间的了解:)可是,通常情况下,咱们依然只对能够被正交向量界说的空间感兴趣。在这一章,咱们将看到正交的许多优美性质,如何求出空间的正交基,以及听起来巨大上的,矩阵的QR分化。…
- 视频:10-1 正交基与规范正交基 (16:48)
- 视频:10-2 一维投影 (12:05)
- 视频:10-3 高维投影和Gram-Schmidt进程 (16:02)
- 视频:10-4 完成Gram-Schmidt进程 (15:59)
- 视频:10-5 规范正交基的性质 (10:39)
- 视频:10-6 矩阵的QR分化 (18:02)
- 视频:10-7 完成矩阵的QR分化 (08:20)
- 视频:10-8 本章小结和更多和投影相关的论题 (08:09)
-
第11章 坐标转化和线性改换5 节 | 75分钟
在之前的学习,咱们深化了解了空间,咱们知道了一个空间能够对应无数组基。在这一章,咱们就将讨论这些基之间的关系——即坐标转化。与此同时,咱们将看到线性代数范畴,对线性改换的谨慎数学界说。
- 视频:11-1 空间的基和坐标系 (14:28)
- 视频:11-2 其他坐标系与规范坐标系的转化 (10:07)
- 视频:11-3 任意坐标系转化 (17:19)
- 视频:11-4 线性改换 (19:52)
- 视频:11-5 更多和坐标转化和线性改换相关的论题 (12:25)
-
第12章 行列式8 节 | 119分钟
行列式是在线性代数的国际里,被界说的另一类根本元素。在这一章,咱们将学习什么是行列式,以及行列式的根本运算规则,为后续两章学习愈加重要的线性代数内容,打下坚实的根底!
- 视频:12-1 什么是行列式 (22:51)
- 视频:12-2 行列式的四大根本性质 (12:55)
- 视频:12-3 行列式与矩阵的逆 (16:35)
- 视频:12-4 核算行列式的算法 (17:21)
- 视频:12-5 初等矩阵与行列式 (17:29)
- 视频:12-6 行式就是列式! (12:42)
- 视频:12-7 虚有其表的行列式的代数表达 (18:20)
- 作业:12-8 关于行列式的编程完成
-
第13章 特征值与特征向量11 节 | 165分钟
特征值和特征向量,或许是线性代数的国际中,最为著名的内容了。究竟什么是特征值?什么是特征向量?咱们为什么要研讨特征值和特征向量?在这一章都将一一揭晓。
- 视频:13-1 什么是特征值和特征向量 (19:38)
- 视频:13-2 特征值和特征向量的相关概念 (14:09)
- 视频:13-3 特征值与特征向量的性质 (15:59)
- 视频:13-4 直观了解特征值与特征向量 (20:20)
- 视频:13-5 “不简略”的特征值 (16:09)
- 视频:13-6 实践numpy中求解特征值和特征向量 (13:55)
- 视频:13-7 矩阵类似和背面的重要意义 (19:58)
- 作业:13-8 换一个视点了解矩阵的类似
- 视频:13-9 矩阵对角化 (15:35)
- 视频:13-10 完成属于自己的矩阵对角化 (14:48)
- 视频:13-11 矩阵对角化的运用:求解矩阵的幂和动态体系 (13:53)
-
第14章 对称矩阵与矩阵的SVD分化7 节 | 103分钟
在学习了特征值与特征向量以后,咱们将在这一章,看线性代数范畴中一类特殊的矩阵——对称矩阵,从而,咱们将来深化分析学习或许是线性代数的国际中,最为重要一个矩阵分化方式——SVD。
- 视频:14-1 完美的对称矩阵 (11:06)
- 视频:14-2 正交对角化 (17:17)
- 视频:14-3 什么是奇特值 (13:32)
- 视频:14-4 奇特值的几许意义 (14:35)
- 视频:14-5 奇特值的SVD分化 (20:00)
- 视频:14-6 实践scipy中的SVD分化 (09:31)
- 视频:14-7 SVD分化的运用 (16:51)
-
第15章 更宽广的线性代数国际,咱们加油!1 节 | 12分钟
恭喜咱们完成了这门课程的学习。在学习完这门课程之后,假如想深化线性代数的国际,还能够向哪些方向探究?这一末节就将向咱们介绍更宽广的线性代数国际!祝咱们收成多多,前进多多,完成心中的愿望。咱们加油!
- 视频:15-1 更宽广的线性代数国际,咱们加油! (11:38)









